Optimal control, trajectory optimization, and getting a rocket to space

11 Jan 2024

Let’s say we wanted to get a rocket to orbit - based on experience (or, if you’ve made it through the Kerbal Space Program tutorial like me), you would roughly know that, with the rocket starting at an upward attitude with respect to the center of the Earth, you would want it to gradually tilt over to become increasingly parallel to the surface of the Earth. But what if we wanted to optimize some part of this flight process - let’s say, to make sure that we have as much fuel mass left as possible at the end of the journey? Well, the next thing we’d think about it, what are the factors of the flight that we can control, and how do these controls, on a physical basis, affect the state of the rocket (eg. the position of the rocket, the velocity of the rocket, the mass of the rocket)?

The simplest reducible example that we can think of is a car at rest at a starting position, which we want to get to a final position, also at rest. We specify an objective - for example, that we want it to reach its final position in the shortest possible time - and then ask what series of controls (applied forces) would optimize that objective. Intuitively, we would say - apply the maximum amount of force possible to get it to accelerate, before the applying the maximum amount of force possible in the opposite direction to get it to decelerate - and indeed, bang-bang solutions are an optimal control.

There are a few special cases where analytical solutions can be found, but most don’t. This brings us to the field of numerical methods to approximate optimal control solutions - one of which is known as trajectory optimization!

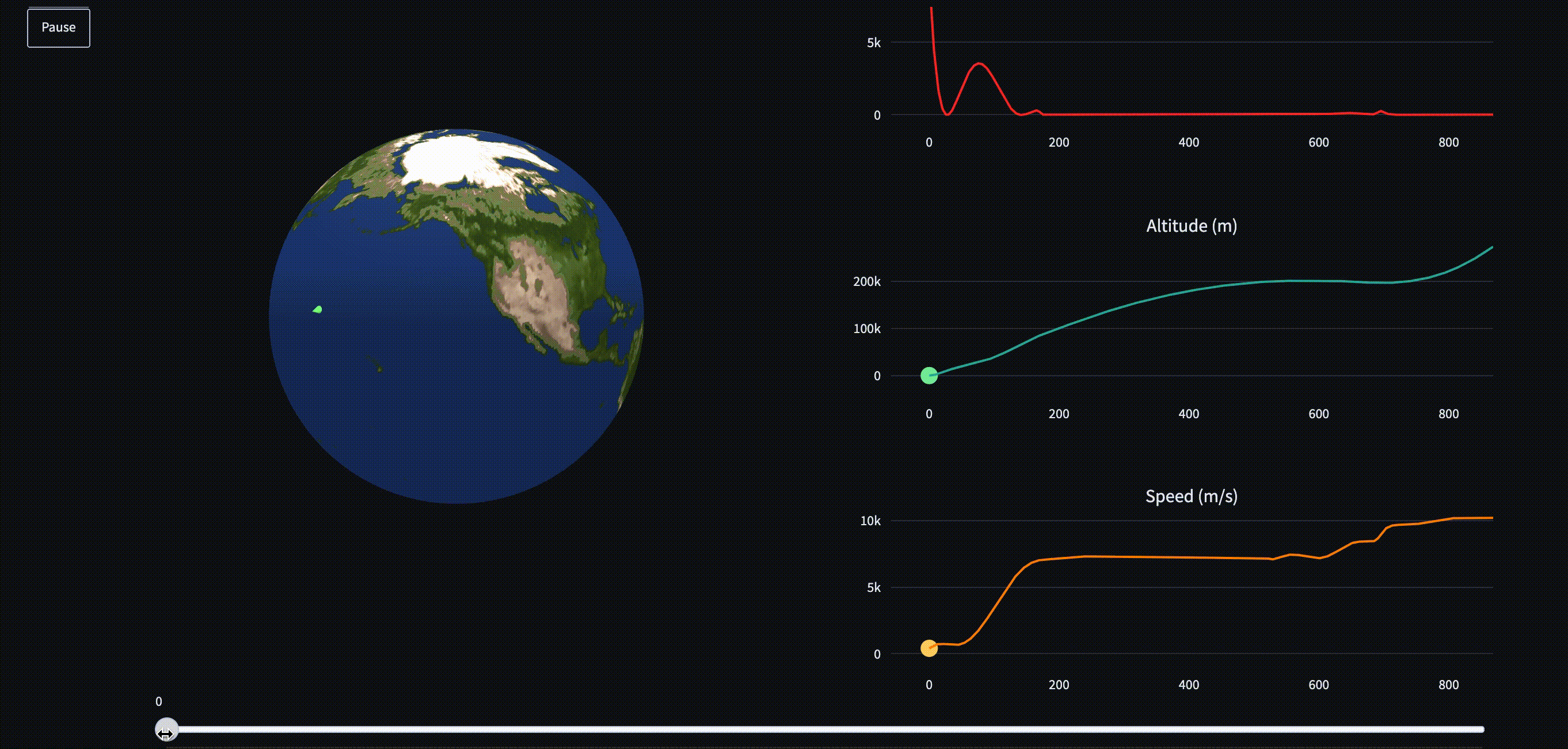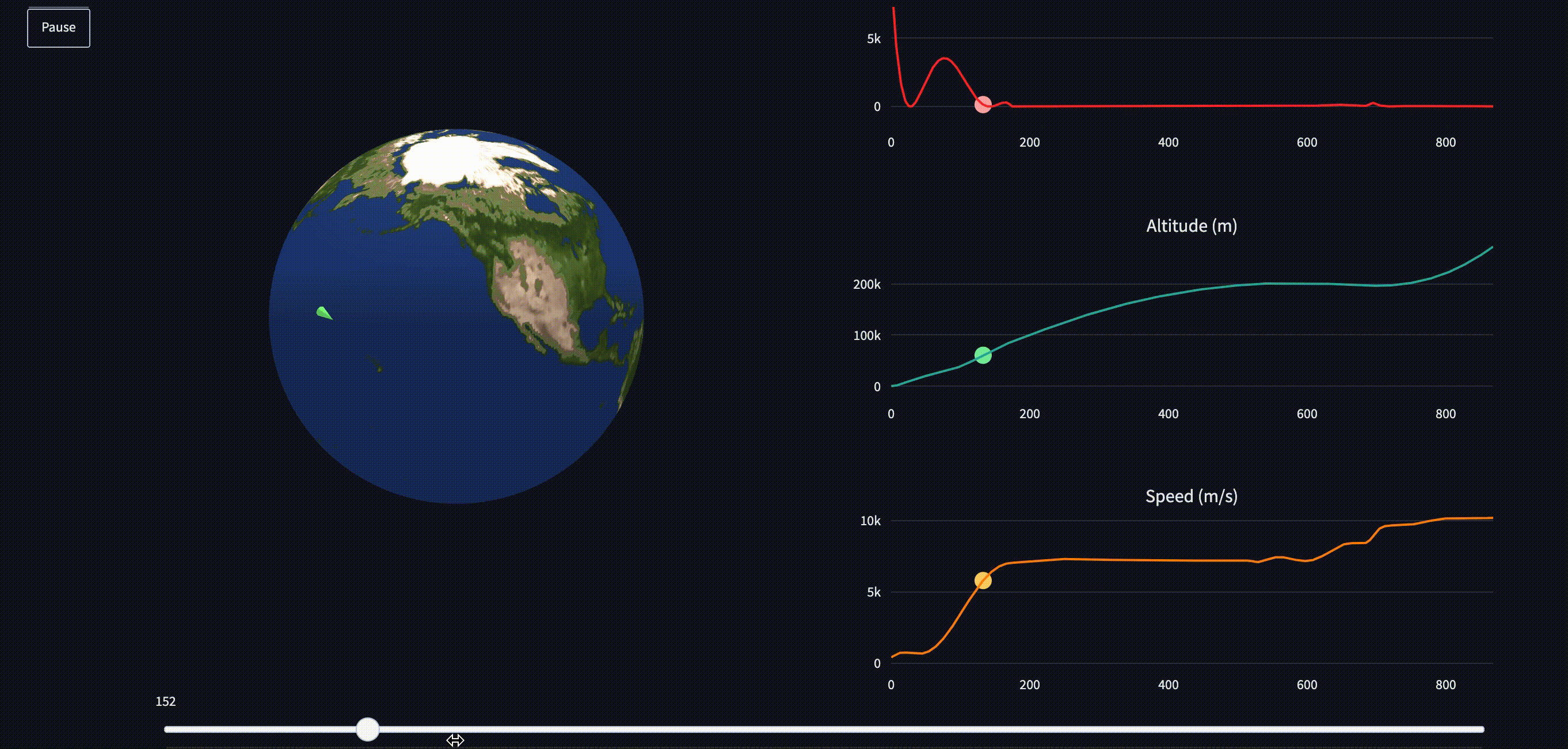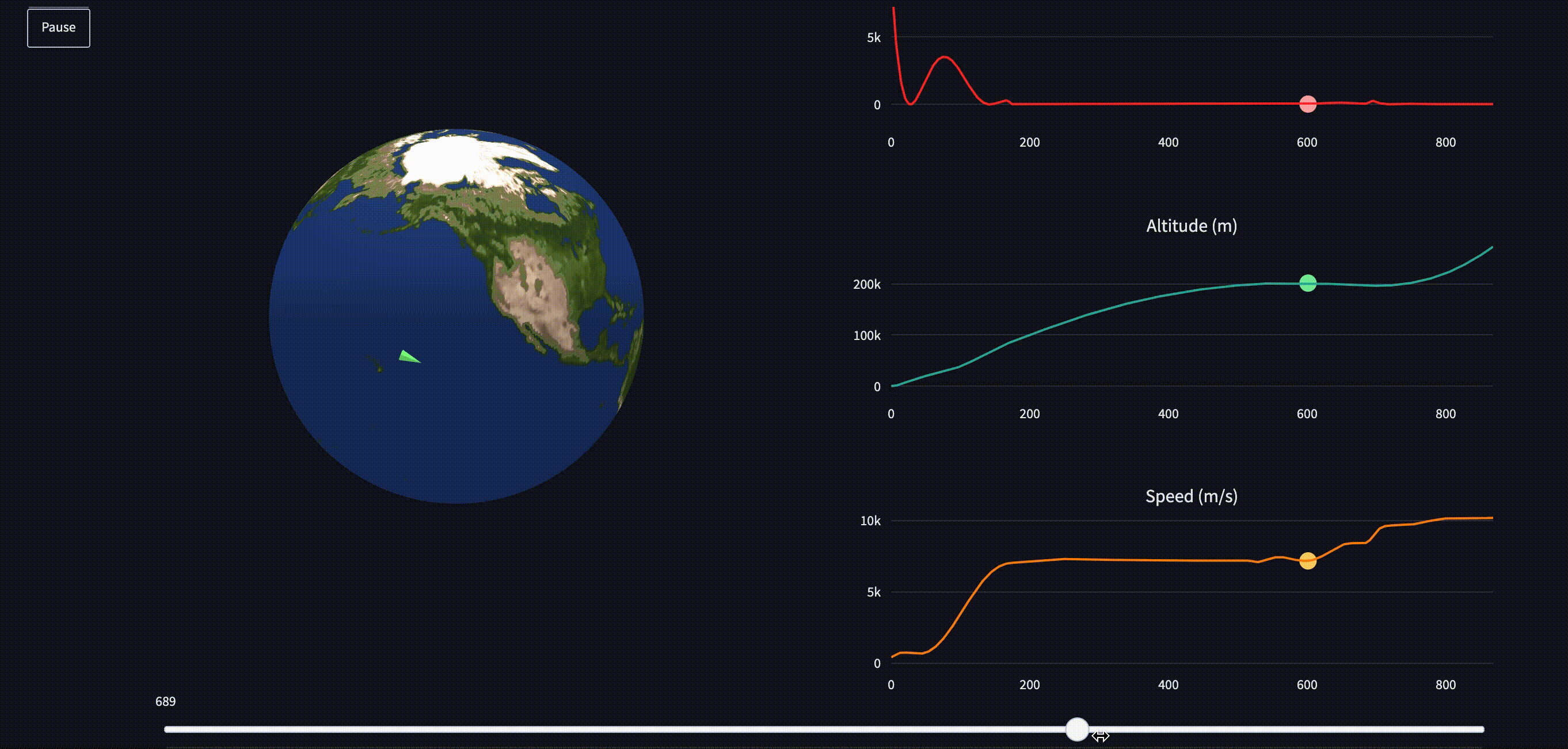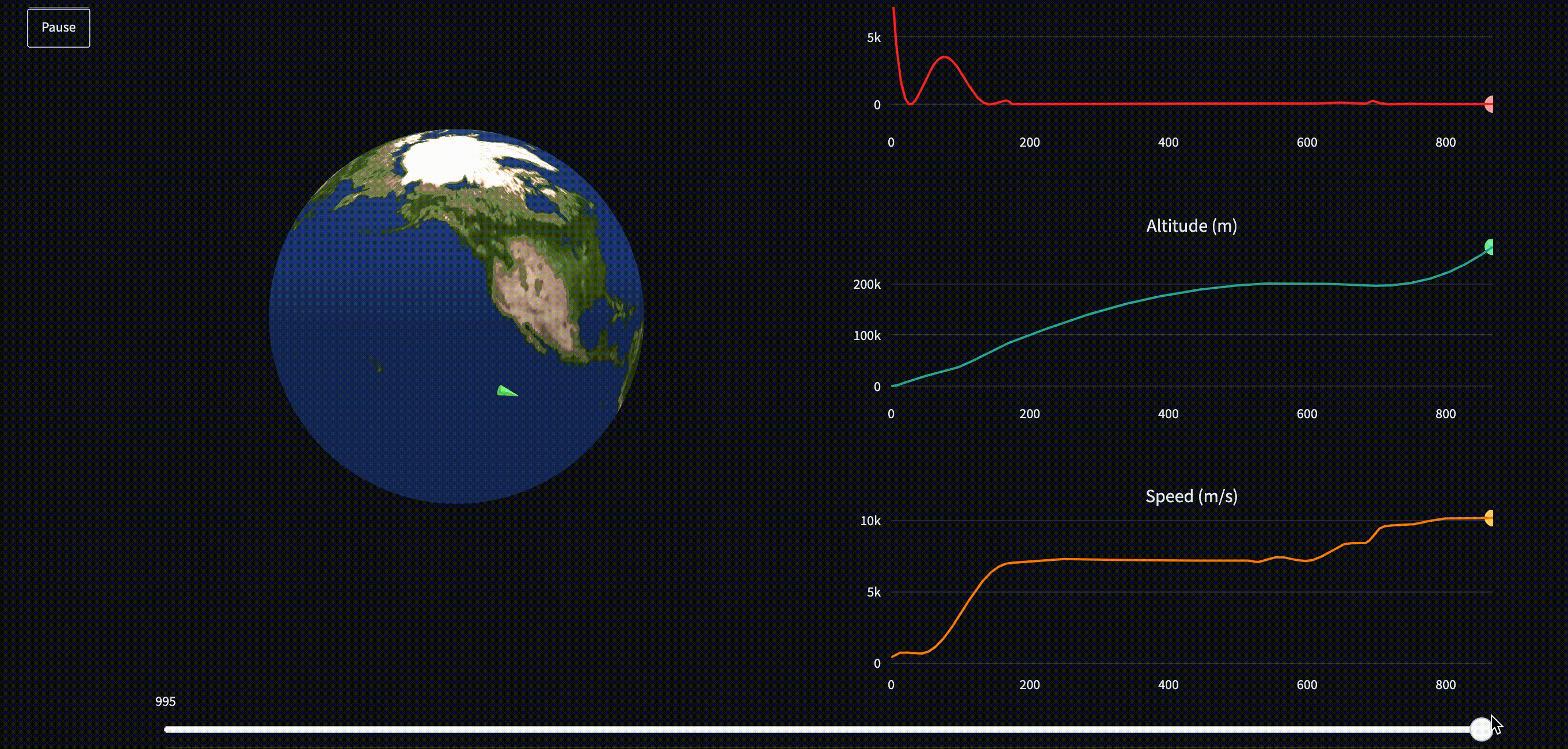
In this app, I display the optimal control trajectory, given a starting position and final desired orbital parameters, using an algorithm known as trajectory optimization. You can try it here.

Mathy stuff if you like it

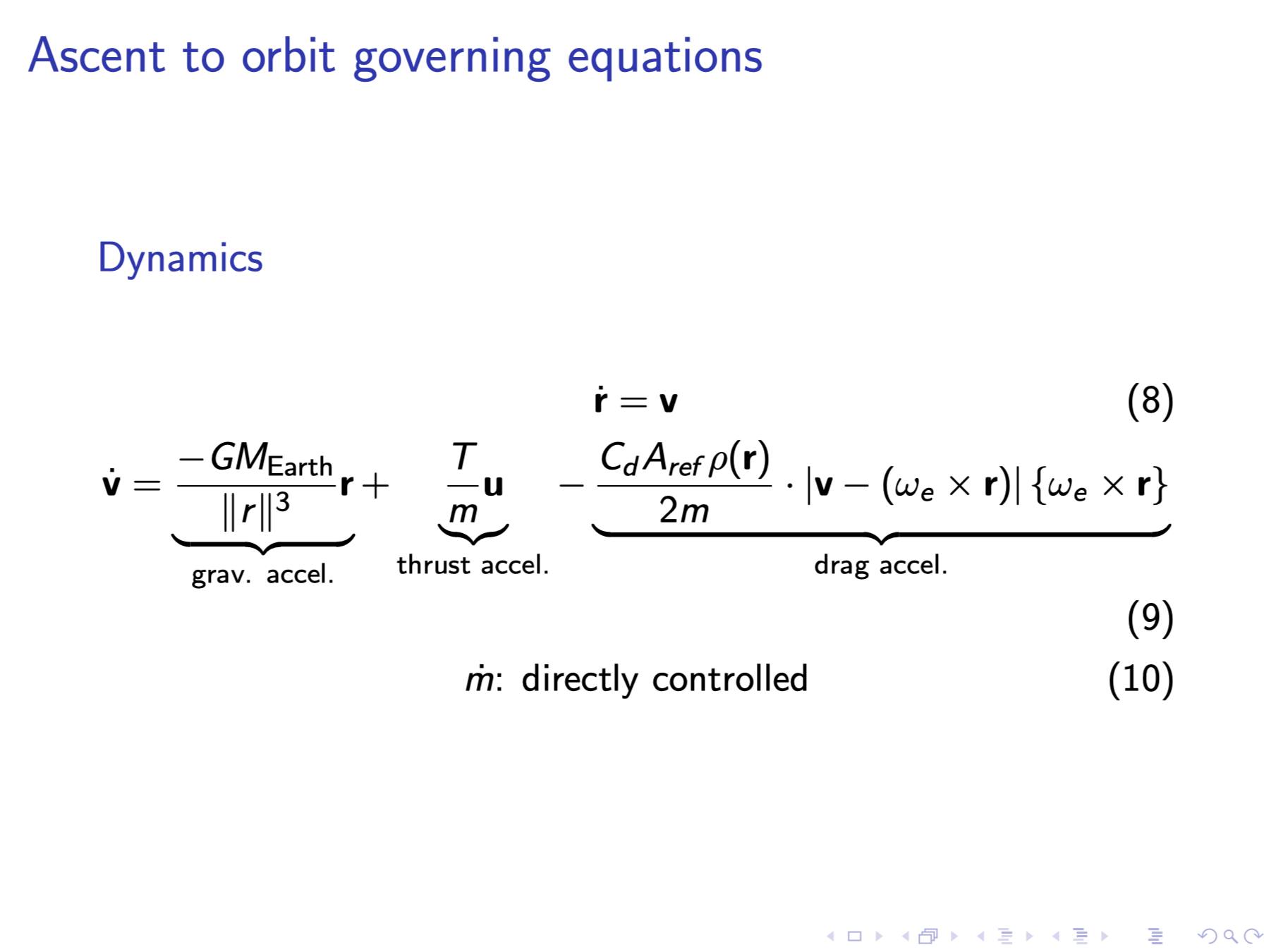
In this section, I outline the optimal control problem specifically: